“I would love to be able to see Einstein’s face right now,” says Rainer Weiss, the co-founder of LIGO.
In 2015, the laser interferometer gravitational-wave observatory(LIGO) discovered its first wave after two black holes collided in space, each about 30 times our sun in mass. Before this, the LIGO gravitational wave project scientists gathered terabytes of data daily to figure out gravitational waves among others in the cosmos. When you imagine a terabyte of data as a second, it will take about 32 thousand years to reach a terabyte — big and complex observational data, indeed. However, analyzing this volume of complex data requires a rigorous computing programming library. LIGO employs Numpy as one of its computational tools in analyzing this ocean of gravitational wave data.
What’s Numpy?

As you know, data comes in several forms: images, videos, audio, or texts. But to make these data analyzable, they must be transformed into an array of numbers. Numpy, short for numerical python, is a Python library package that helps to compute and analyze arrays using various mathematical and logical functions.
Why Numpy?
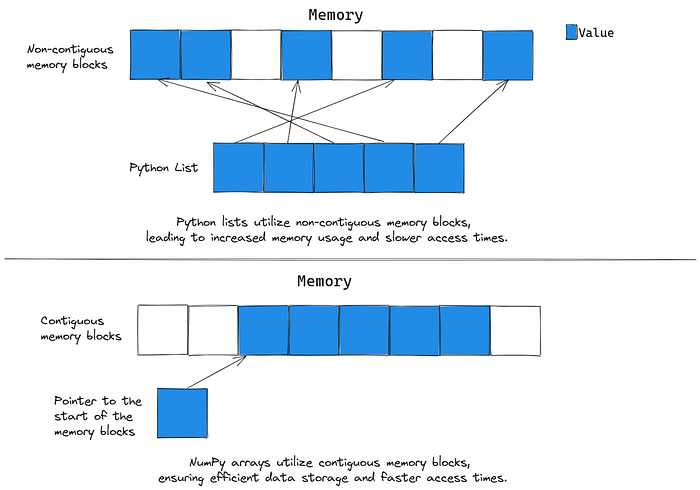
Unlike regular Python lists, Numpy is faster for scientific computing and data manipulation. Numpy arrays are implemented in C programming. This makes it the best fit for high-performance computing as it performs parallel computing on homogenous data arrays and stores them in contiguous order on the computer memory for easy accessibility. A Numpy array can only contain all strings, floats, or integers as elements. When you store a heterogeneous data type in a Numpy array, for instance, an integer data type with a floating points array, Numpy will automatically upcast the integer to a floating data type to maintain its homogeneity.
However, a Python list can store heterogeneous data types. You loop over each element to perform a repetitive task in a list. Python stores each element in various blocks across the computer memory. For you to access all these elements, the Python list will iterate through the scattered elements, which takes a longer runtime and poor performance in larger datasets.
Creating Numpy arrays
Before creating a Numpy array, you must install the Numpy library on your system. You can do so using the pip installer package, which handles the Numpy installation and its dependency.
pip install numpy
Verify your installation using
pip show numpy
Now, create your first Numpy array using the array() method
import numpy as np
# Create a 1D array from 1 to 5
first_array = np.array([1,2,3,4,5])
print(first_array)
print(type(first_array.dtype)) # for showing the data type
output:
[1 2 3 4 5]
<class 'numpy.dtype[int32]'>
“I actually sacrificed tenure at a university to write Numpy and unify array objects.” Travis Oliphant (Numpy creator).
Dimensions and Shapes in NumPy array
All Numpy arrays have dimensions– from zero, one, two, and three to higher dimensional arrays. A dimension of an array is the number of axes it has. For instance, a 0-D array is a scalar array with a single value with no axes, while a 1D array is a vector array with only one axis. Likewise, a 2-D array has two axes, say rows and columns, and a 3-D array has three axes say rows, columns, and depth. You can determine the dimension of an array using the .ndim attribute.
The shape of an array, however, is a tuple that represents the size of each dimension of an array. Use the .shape attribute to determine the shape of an array.

Let’s create dimensional arrays in Numpy and determine their shapes
import numpy as np
# Create 0,1,2 dimensional arrays
zero_dim = np.array(42)
one_dim = np.array([1, 2, 3, 4, 5])
two_dim = np.array([[1, 2, 3], [4, 5, 6]])
# Determine dimensions
print("zero_dim_array:", zero_dim.ndim)
print("one_dim_array:", one_dim.ndim)
print("two_dim_array:", two_dim.ndim)
# Determine the shape
print("zero_dim_array shape:", zero_dim.shape)
print("one_dim_array shape:", one_dim.shape)
print("two_dim_array shape:", two_dim.shape)
outputs:
zero_dim_array: 0
one_dim_array: 1
two_dim_array: 2
zero_dim_array shape: ()
one_dim_array shape: (5,)
two_dim_array shape: (2, 3)
Indexing and Slicing
Like the Python list, you can access Numpy array elements using indexing and slicing. Numpy index the first element as the 0th index while the nth element is (n-1)th index. However, array slicing requires specifying the start, end, and step. Remember, the end index is always exclusive.
Let’s take some examples:
import numpy as np
# Accessing the 5th element (index 4) from a 1D array
arr = np.array([15, 25, 35, 45, 55])
print(arr[4])
# Accessing the 1st three row elements from a 2D array
arr2 = np.array([[2,4,6],[8,10,12]])
print(arr2[0,0]) # 2
print(arr2[0,1]) # 4
print(arr2[0,2]) # 6
# Accessing the last element in a 1D array using negative indexing
arr3 = np.array([15, 25, 35, 45, 55])
print(arr3[-1]) # 55
import numpy as np
# Slicing from index 2 to 5 (remember index 5 will be excluded)
arr = np.array([5, 10, 6, 8, 4, 7, 3, 2])
print(arr[2:5]) # output [6 8 4]
# Slicing from index 4 to the last
arr1 = np.array([9, 10, 6, 8, 4, 7, 3, 2])
print(arr1[4:]) # output [4 7 3 2]
# Slicing from the 1st index to the 5th (the 5th index will be excluded)
arr2 = np.array([15, 10, 6, 8, 4, 7, 3, 2])
print(arr2[:5]) # output [ 15 10 6 8 4]
# Slicing from index 1 to 8 with 2 steps
arr3 = np.array([1, 10, 6, 8, 4, 7, 3, 2])
print(arr3[1:8:2]) # output [10 8 7 2]
Operations on NumPy arrays
Numpy performs complex mathematical and data manipulation operations such as statistical analysis, linear algebra, and universal functions. Let‘s see some examples:
Statistical operations
Numpy can compute the mean, median, standard deviation, percentile, and other statistical functions.
# Create a 1D arrays: arr1
arr1 = np.array([1, 2, 3, 4, 5])
# calculating the mean values of the arrays
arr_mean = np.mean(arr1)
# calculating the median values of the arrays
arr_med= np.median(arr1)
# calculating the standard deviation of the arrays
arr_std = np.std(arr1)
# calculating the maximum and minimum of the arrays
arr_min = np.min(arr1)
arr_max = np.max(arr1)
# calculating the 25th and 75th percentile of the arrays
arr_percent1 = np.percentile(arr1, 25)
arr_percent2 = np.percentile(arr1, 75)
print("mean:",arr_mean)
print("median:",arr_med)
print("standard deviation:",arr_std)
print("minimum value:",arr_min)
print("maximum value:",arr_max)
print("25th percentile:",arr_percent1)
print("75th percentile:",arr_percent2)
Outputs:
mean: 3.0
median: 3.0
standard deviation: 1.4142135623730951
minimum value: 1
maximum value: 5
25th percentile: 2.0
75th percentile: 4.0
To calculate the median, mean, and standard deviation for an N-d array, say 2-D, like arr2 and arr3, you need to specify the axis — vertical or horizontal. Use axis=0 as a parameter in np.medium() for the vertical axis while 1 for the medium value along the horizontal axis. However, if you don’t specify any axis in the medium function, Numpy computes the medium throughout the array.
import numpy as np
arr2 = np.array([[10, 15, 20],
[25,30,35],
[40,45,50]])
arr3 = np.array([[3,2],
[4,5]])
# median along horizontal axis
med1 = np.median(arr2, axis=1)
print("Median along horizontal axis:", med1)
# median along vertical axis
med2 = np.median(arr2, axis=0)
print("Median along vertical axis:", med2)
# median of the entire array
med3 = np.median(arr2)
print("Median of entire array:", med3)
Outputs:
Median along horizontal axis: [15. 30. 45.]
Median along vertical axis: [25. 30. 35.]
Median of entire array: 30.0
# mean along horizontal axis
mean1 = np.mean(arr3, axis=1)
print("Mean along horizontal axis:", mean1)
# mean along vertical axis
mean2 = np.mean(arr3, axis=0)
print("Mean along vertical axis:", mean2)
# median of entire array
mean3 = np.mean(arr3)
print("Mean of entire array:", mean3)
Outputs:
Mean along horizontal axis: [2.5 4.5]
Mean along vertical axis: [3.5 3.5]
Mean of entire array: 3.5
Try out the standard deviation for arr3. Did you get this output?
std along horizontal axis: [0.5 0.5]
std along vertical axis: [0.5 1.5]
std of entire array: 1.118033988749895
Numpy was created to merge array objects in Python and unify Pydata community. Travis Oliphant, Numpy creator.
Arithmetic operations
Numpy can handle basic arithmetics such as addition, subtraction, multiplication, and division efficiently element-wise in less time.
import numpy as np
# Create arrays
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Add the elements of the array
add_arr = np.sum([arr1, arr2])
print("Sum = ", add_arr)
# Add the array elements using the axis parameter
add_col = np.sum([arr1, arr2], axis = 0) # adding in column-wise
add_row = np.sum([arr1, arr2], axis = 1) # adding in row-wise
print("Column_Sum = ", add_col)
print("row_Sum = ", add_row)
# Subtract the arrays elements
sub_arr = np.subtract(arr1, arr2)
print("Subtraction = ", sub_arr)
# Multiply the elements of the arrays
mul_arr = np.multiply(arr1, arr2)
print("Multiplication = ", mul_arr)
# Divide the elements of the array
div_arr = np.divide(arr1, arr2)
print("Division = ", div_arr)
Outputs:
Sum = 36
Column_Sum = [ 6 8 10 12]
row_Sum = [10 26]
Subtraction = [-4 -4 -4 -4]
Multiplication = [ 5 12 21 32]
Division = [0.2 0.33333333 0.42857143 0.5 ]
What’s More?
Some of the things I discussed here are the tip of the iceberg in Numpy. You can gather further information about Numpy by doing an online search, reading the Numpy documentation, and playing with some exercises.
Thanks for coming this far!
Connect with me on Linkedin or by mail for any questions or suggestions.
Stay curious, stay persistent, and enjoy the satisfaction of solving problems. Happy learning!

